陈瑞娴同学在相位调制全息存储研究中获得新进展
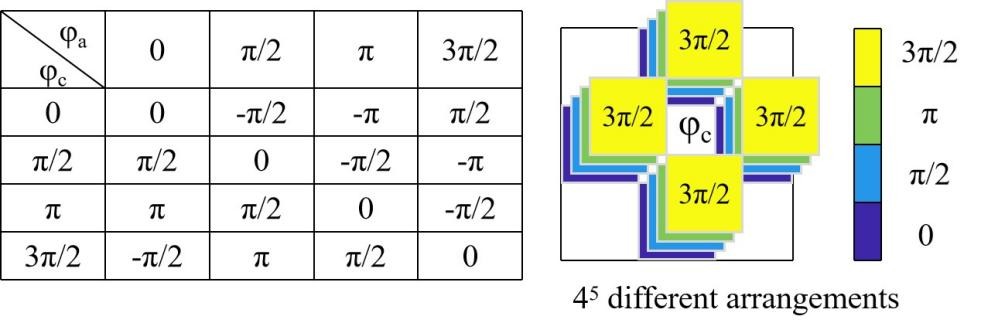
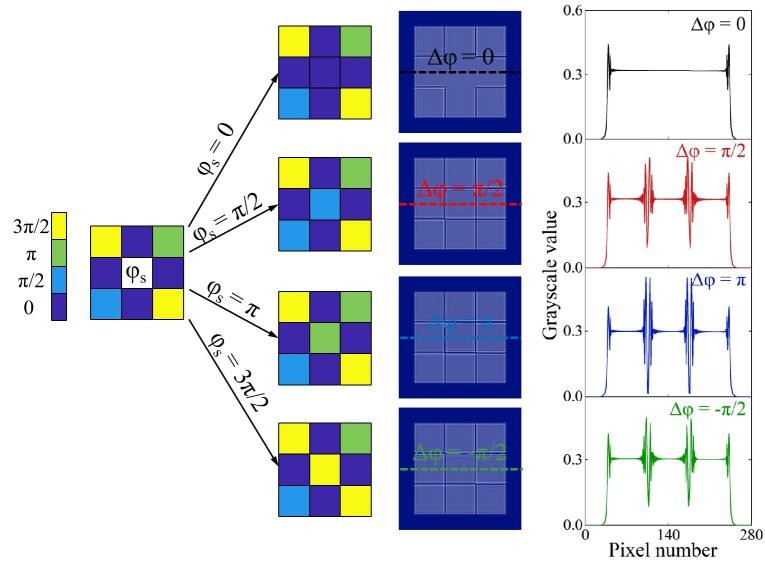
全息数据存储(Holographic Data Storage, HDS)通过将信息存储在三维介质中,并以二维数据页的形式处理信息,拥有高容量和高传输速率的优势。其中相位型HDS因其较高的信噪比而备受关注,但相位信息无法直接通过探测器检测。近年来,深度学习在解决计算成像中的逆问题方面表现出色,为HDS中的相位重建提供了新的解决方案。本文提出了一种基于深度学习的嵌入式数据相位重建方法,在减少大量训练样本需求的情况下,同时提高HDS系统中相位重建性能。 以4级相位编码为例,中心数据(φc)和相邻数据点(φa)之间的相位差(Δφ=φc-φa)如图1所示,所有相位差都转换到[-π,π]的范围内。可以看出,每个中心数据有四个可能的相邻相位值,导致4^5种不同的排列。因此,为了进行准确的相位预测,通常需要一个广泛地覆盖各种数据排列的训练数据集。然而,在HDS系统中,获取大量标记样本而导致的材料过度消耗。此外,信息的存储会导致材料收缩和噪声分布不均,从而导致样本质量下降。为了减少对大量标记样本的依赖并提高抗噪性,本研究提出了一种基于深度学习的嵌入式数据相位重建方法。本文提出的方法利用已知的嵌入式数据作为强约束,在多阶相位编码的情况下,每个信号数据相对于嵌入式数据的相位差具有唯一解。在图2中,可以观察到每个信号相位都被相同的已知相位包围,导致只有4种不同的排列。这种创新的编码策略将信号数据及其相邻数据的排列从4^5种减少到仅4种,使得单个标记样本可以包含所有可能的编码排列。 |
|
| 图1. 编码规则下可能存在的相位差和排列 |
|
| 图2. 4种数据排列和相应的衍射强度图像 |
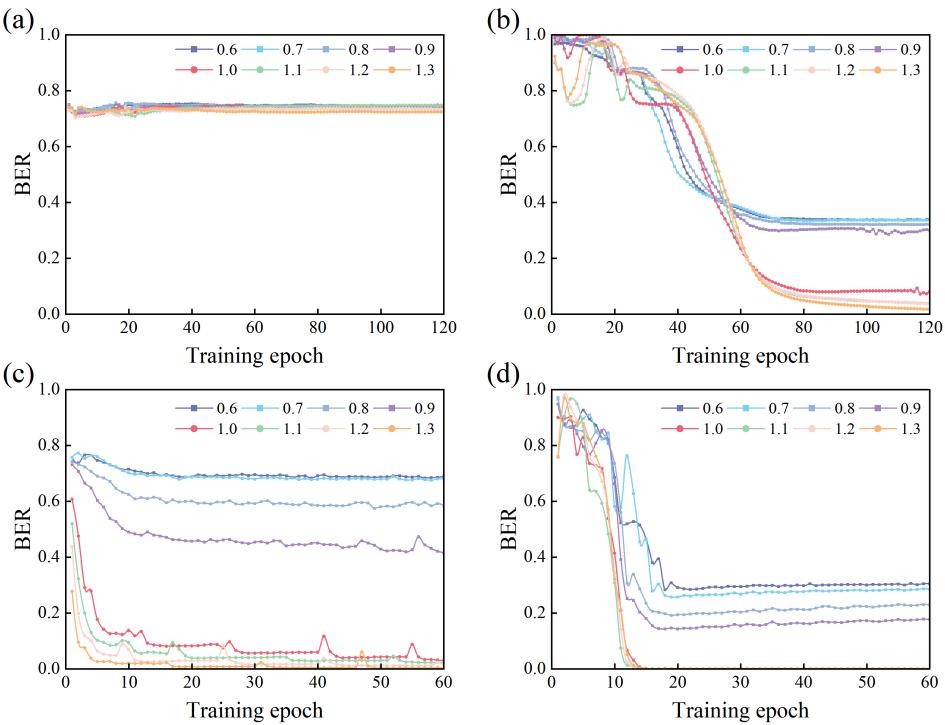
由于嵌入数据对衍射强度图像施加的鲁棒约束,即使记录介质中的全息图尺寸限制在奈奎斯特大小,导致边缘模糊,我们的方法仍然可以实现精确的相位重建。我们模拟不同奈奎斯特比率(NR)下,比较传统方法和所提方法的相位重建结果,如图3所示。当只有一对训练样本并且前提上没有强约束时,深度学习模型无法从有限的样本中实现良好的泛化。嵌入式数据可以为样本提供强有力的约束,使单个样本可以包含所有可能的数据排列。此外,在这种编码策略中,衍射强度图像只有四种相位差,因此即使高频信息丢失,只要NR大于或等于1,就可以更准确地检索信息。为了进一步提高精度,在NR=1.0时,没有嵌入数据的样本需要增加到1000,BER为0.0302。在NR=1.0时,嵌入数据的训练样本只需要增加到20,BER就能达到0.0003。相比之下,所提出的方法需要更少的训练样本,BER更低。 |
|
| 图3. 不同NR下的相位重建模拟结果(a)训练集为1,训练样本无嵌入式数据 (b)训练集为1,训练样本有嵌入式数据(c)训练集为1000, 训练样本无嵌入式数据(d)训练集为20,训练样本有嵌入式数据 |
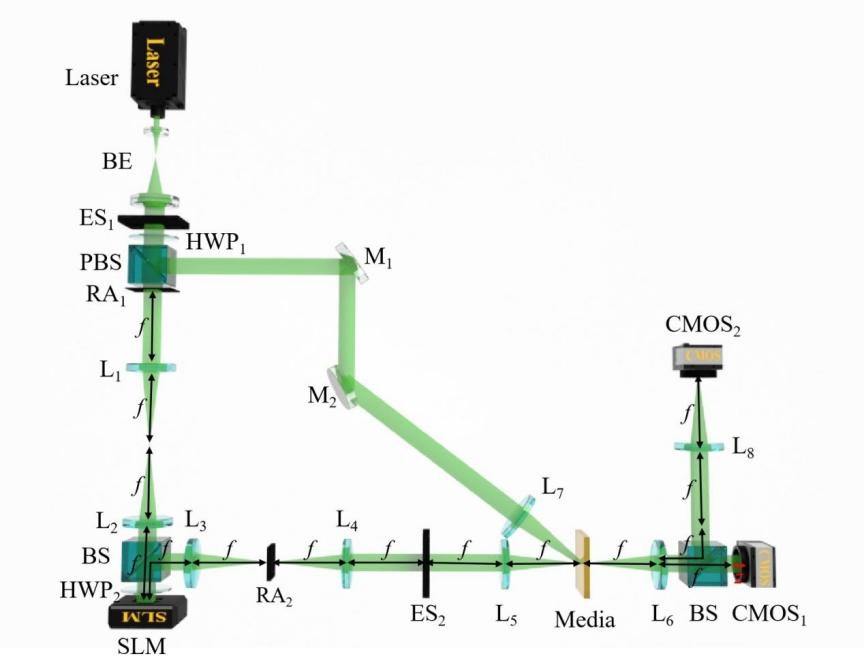
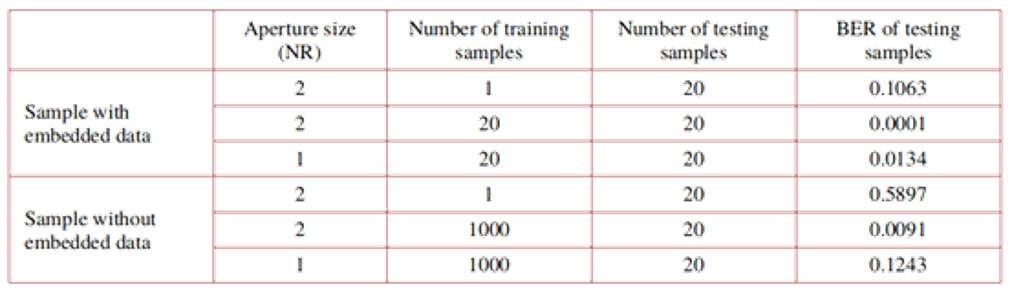
实验光路如图4所示。表1是不同NR和训练样本数量下,传统方法和本文所提方法的比较。首先,当NR设置为2,两种方法的训练样本数均为1时,传统方法和所提方法的BER分别为0.5897和0.1063。由于实验环境中的复杂噪声,这两种方法都表现出较高的BER。然而,所提方法的BER相对更低。其次,为了有效降低误码率,我们可以增加训练样本的数量。具体来说,本文提出的方法仅需20对训练样本即可将BER降至0.0001,而相比之下,传统方法需要1000对训练样本才能将BER降至0.0091。由于嵌入数据对衍射强度图像施加的鲁棒约束,可以实现更小的记录全息图尺寸,从而提高存储密度。当NR设置为1时,这意味着介质的记录区域仅为奈奎斯特大小。当模型用20对样本训练时,本文提出的方法可以将BER降低到0.0134,而传统方法即使使用1000对样本进行训练,也只能将BER降至0.1243。通过比较实验结果,我们发现当记录区域仅为奈奎斯特大小时,与传统方法相比,所提方法需要的训练样本减少了约50倍,而BER降低了约9倍。 |
|
| 图4. 相位型全息存储系统示意图 |
| 表1. 不同NR和训练样本数量下,传统方法和本文所提方法的比较 |
|
上述研究成果以“Deep learning-based phase retrieval with embedded data for holographic data storage”为题,整理发表在美国光学学会 (The Optical Society of American, OPTICA) 期刊杂志 Optics Express, Vol.33, No.6, 12731-12746 (2025)上。 论文的相关链接:https://doi.org/10.1364/OE.554607 |

|
(2025.03.11)
